Remember the quadratic formula? Given ax²+bx+c=0, the solution is $x=(-b±√(b^2-4ac))/(2a)$, which may have felt arduous to memorize in high school, but you have to admit is a conveniently closed-form solution.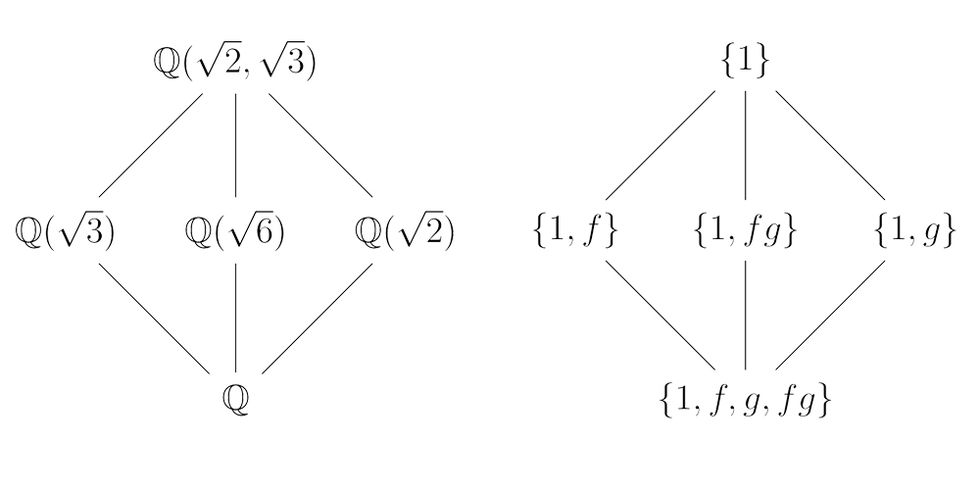

Now, if we go up to $ax³+bx²+cx+d=0$, a closed form for “x=” is possible to find, although it’s much bulkier than the quadratic version. It’s also possible, yet ugly, to do this for degree $4$ polynomials $ax⁴+bx³+cx²+dx+f=0$.
The goal of doing this for polynomials of any degree was noted as early as the 15th century. But from degree $5$ on, a closed form is not possible. Writing the forms when they’re possible is one thing, but how did mathematicians prove it’s not possible from 5 up?
The world was only starting to comprehend the brilliance of French mathematician Evariste Galois when he died at the age of $20$ in $1832$. His life included months spent in prison, where he was punished for his political activism, writing ingenious, yet unrefined mathematics to scholars, and it ended in a fatal duel.
Galois’ ideas took decades after his death to be fully understood, but eventually they developed into an entire theory now called Galois Theory. A major theorem in this theory gives exact conditions for when a polynomial can be “solved by radicals,” meaning it has a closed form like the quadratic formula. All polynomials up to degree 4 satisfy these conditions, but starting at degree $5$, some don’t, and so there’s no general form for a solution for any degree higher than $4$.
Πηγή: popularmechanics

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου