Example of using Partial Fraction to evaluate Integral
Example of using Partial Fraction to evaluate Integral |
Problem We like to evaluate the integral: 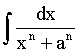 where n = 1, 2, 3, 4. We employ the technique of Partial Fractions. This algebraic method is assumed to be known. |
When n = 1, 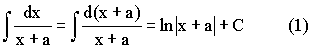 |
When n = 2, By using the substitution x = tan q, it is a simple exercise to get: 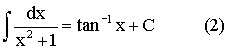 Then, 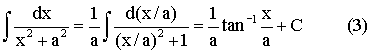 In getting (3) here, we change the variable and apply (2). Alternatively, you can start by using the substitution x = a tan q at the beginning of (3). |
When n = 3, 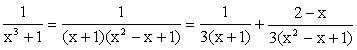
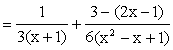 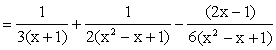 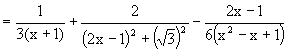 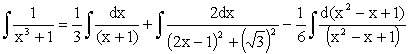
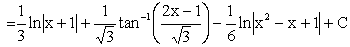 |
|
Finally you may check by changing the valuable suitably: 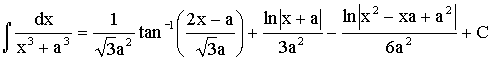
|
When n = 4, Since x4 + 1 cannot be factorized under rational numbers, we start with the factorization : x4 + 1 = (x4 + 2x2 + 1) – 2x2 = (x2 + 1)2 – (Ö2 x)2 = (x2 + Ö2 x + 1)(x2 -Ö2 x +1) As a Partial Fraction exercise, we get: 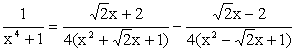 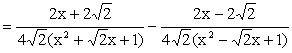 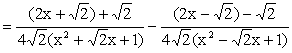 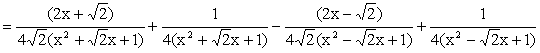 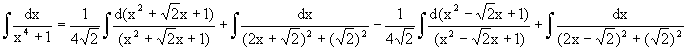
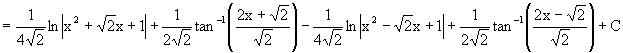 Finally, if you still feel energetic of checking, we arrive: 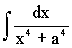
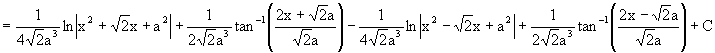
|

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου