Οπτικοποιώντας το Ολοκλήρωμα Dirichlet

Το ολοκλήρωμα

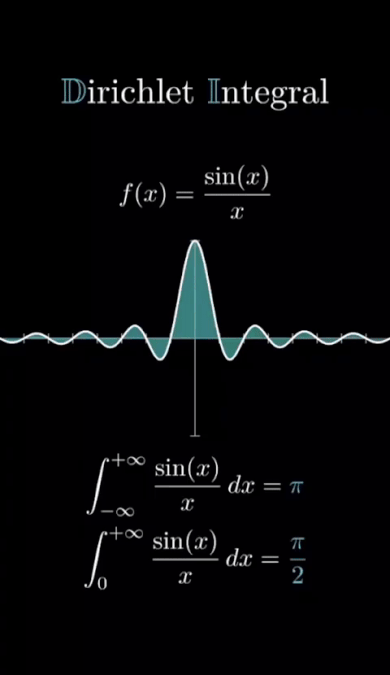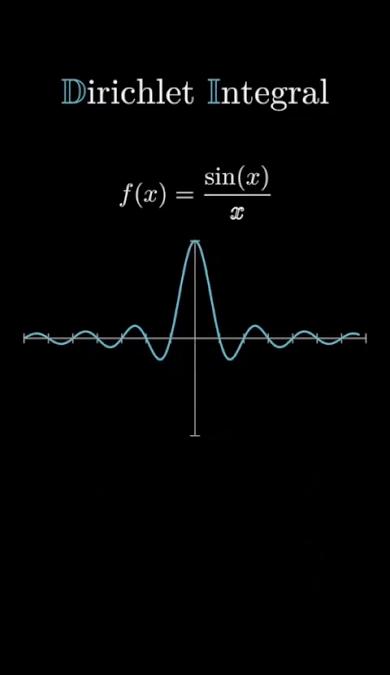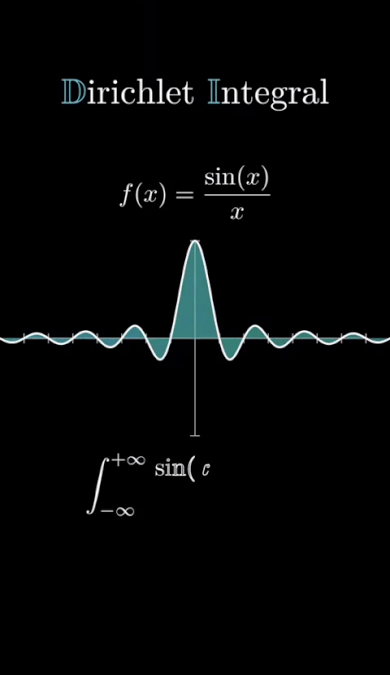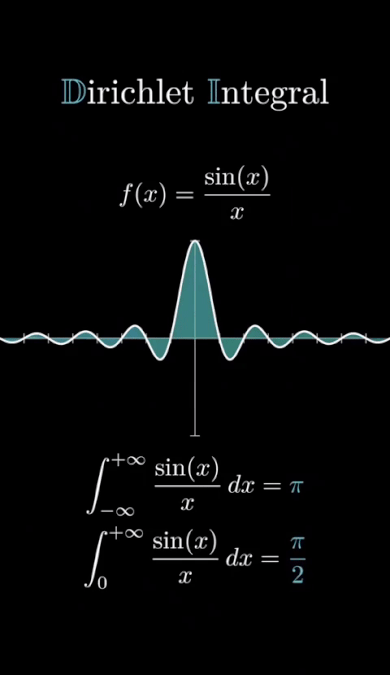
$$\int_0^{\infty} \frac{\sin x}{x} \, dx = \frac{\pi}{2}$$είναι μια από τις πιο όμορφες και παράξενες εκφράσεις στα μαθηματικά.

▶️ Στο βίντεο βλέπουμε την καμπύλη της συνάρτησης

$$f(x) = \frac{\sin x}{x}$$που ταλαντώνεται γύρω από τον άξονα $x$, αλλά με μειούμενο πλάτος.

🌀 Αν και η γραφική έχει άπειρες εναλλαγές πρόσημου, το συνολικό (υπογεγραμμένο) εμβαδόν κάτω από τη συνάρτηση συγκλίνει σε μια πεπερασμένη τιμή — το $\dfrac{\pi}{2}$​!

➡️ Αυτή η οπτικοποίηση μας βοηθά να καταλάβουμε πώς μια συνάρτηση με άπειρες ταλαντώσεις και αργή μείωση πλάτους «συνοψίζεται» σε μια συγκεκριμένη σταθερά.